
Votre fournisseur cloud est-il vraiment durable?
Les conséquences de nos actions ou de notre inaction d’aujourd’hui ne feront que se multiplier au fil du temps. Alors demandons-nous: mon fournisseur cloud est-il vraiment durable ?

Dans un monde dominé par "la data", les GPU sont le hardware de référence pour l’entrainement de modèles de deep learning. Mais qu’en est-il des tâches qui ne nécessitent pas forcement le recours à un « artificial neural network » ? Dans le cas un moteur de recommandation par exemple, l'utilisation d'un GPU est-elle pertinente ? C’est ce que nous allons voir !
« Les clients ayant appréciés ce produits recommandent également… », « Voici de séries basées sur vos goûts ». Vous êtes sans doute familiers avec ces recommandations reposant sur les caractéristiques d'un produits ou plus souvent sur le comportement d’utilisateurs jugés comme « semblables ».
Imaginons que nous souhaitions mettre en place ce type de moteur de recommandation relativement simple pour recommander des livres. Les données dont nous avons besoin sont disponibles librement sur des sites proposant la critique de livres par ses utilisateurs: c’est par exemple le cas de ce dataset que nous avons trouvé sur BookCrossing.com, un site dont la mission est « releasing books into the wild » - autrement dit qui propose de laisser des livres dans des lieux publics pour être ramassés et lus par d’autres membres de la communauté. Ces derniers proposent trois tableaux de données disponibles, mais nous n’en aurons besoin que de deux aujourd’hui: BX-Books et BX-Book-Ratings contenant respectivement des informations sur les livres et les notes de ces livres données par les « Bookcrossers »(pardonnez l’utilisation excessive du mot livre dans la phrase précédente , trouver un synonyme approprié n’est pas une tâche facile!). Chaque livre dans BX-Books est identifié par un ISBN unique, et chaque ligne de BX-Book-Ratings répertorie l’ISBN du titre auquel se réfère la note de l’utilisateur.

Avant toute chose, penchons nous plus en détails sur la manière dont les notes peuvent être utilisées pour générer des recommandations de livres pertinentes. Si vous êtes déjà familier avec les bases d'un système de recommandation (ou tout simplement pas intéressé par les détails), n’hésitez pas à passer à la section suivante pour la comparaison CPU vs GPU.
Pour chaque livre, il existe différentes évaluations publiées par différents utilisateurs, et ce sont ces informations que nous utiliserons pour déduire le degré de pertinence de notre moteur. Prenons “Harry Potter et la pierre du sorcier”, “Harry Potter et la chambre des secrets” (les deux premiers tomes de la série) et un manuel intitulé “Calcul quantique et Information quantique”. Pour schématiser, disons que nous avons un total de cinq lecteurs. Quatre d’entre eux ont lu les deux livres de Harry Potter et leur ont donné de bonnes notes. L’un des quatre a également apprécié la lecture d’informations quantiques:
| Reader A | Reader B | Reader C | Reader D | Reader E | |
|---|---|---|---|---|---|
| HP 1 | 7 | 8 | 7 | 9 | 8 |
| HP 2 | 8 | 8 | 9 | 6 | - |
| QCQI | 10 | - | - | - | - |
Eric (justement représenté par la lettre E dans le tableau) a pris comme résolution du Nouvel An de lire davantage en 2020, et, comme souvent, n’a fait aucun effort pour s’y tenir jusqu’au milieu de l’année. Eric lit alors le premier livre de Harry Potter et aimerait utiliser les notes de ses amis pour décider quoi lire ensuite. Comment peut-il faire ça?
Tout d’abord, remplaçons les - (non lus) dans le tableau ci-dessus par des zéros:
| Reader A | Reader B | Reader C | Reader D | Reader E | |
|---|---|---|---|---|---|
| HP1 | 7 | 8 | 7 | 9 | 8 |
| HP2 | 8 | 8 | 9 | 6 | 0 |
| QCQI | 10 | 0 | 0 | 0 | 0 |
A présent, chaque livre correspond à un vecteur de dimension 5 contenant les scores que chaque lecteur lui a attribué. Eric aimerait savoir quel livre parmi le second tome d'Harry Potter ou le manuel d’information quantique serait le plus similaire à Harry Potter 1, en se basant sur les notes des lecteurs. Mathématiquement, cela signifie que nous allons considérer deux paires de vecteurs: HP1 et HP2, et HP1 et QCQI. Un modèle est couramment utilisé pour analyser la similitude de deux vecteurs: la similarité cosinus donnée par le produit scalaire des deux vecteurs divisé par le produit de leur amplitude:
cos(θ) = A·B / ||A|| ||B||
Lorsque deux vecteurs sont alignés l’un avec l’autre, le cosinus de l’angle (zéro) qu'ils forment est 1, ce qui signifie que la similitude est maximisée. La similitude est nulle pour deux vecteurs perpendiculaires (par exemple s’il n’y a pas de chevauchement des courbes chez les utilisateurs qui lisent les deux livres), et peut également être négative si nous avions permis des évaluations négatives dans notre tableau de données. Les cosinus des deux paires en question sont calculés comme suit:
| cos(θ) | ||
|---|---|---|
| HP1 & HP2 | (7x8+8x8+7x9+9x6) / [Sqrt(72+82+72+92+82) Sqrt(82+82+92+62)] | 0.86 |
| HP1 & QCQI | (7x10) / [Sqrt(72+82+72+92+82) Sqrt(102)] | 0.40 |
Ainsi, lorsque nous faisons une recommandation sur le livre à lire en fonction de l’intérêt d’Eric pour Harry Potter et la pierre du sorcier, c’est bien Harry Potter et la chambre des secrets qui ressort gagnant (bien mieux que le calcul quantique et l’information quantique!).
Comme vous pouvez l’imaginer, l’effort pour calculer les similarités cosinus de chaque paire de vecteurs croît assez rapidement avec le nombre de livres et le nombre d’utilisateurs. Voyons d’abord combien de temps cela prendra sur un CPU (un vCPU haut de gamme composé de 10 cœurs Intel Xeon Gold 6148, pour être précis), en utilisant les librairies bien connues pandas and sklearn.
Commençons par importer les données via pandas.
import pandas as pddatadir = 'reco/BX-CSV-Dump/'books = pd.read_csv(datadir+'BX-Books.csv', sep=';', error_bad_lines=False, encoding="latin-1")books.columns = ['ISBN', 'bookTitle', 'bookAuthor', 'yearOfPublication', 'publisher', 'imageUrlS', 'imageUrlM', 'imageUrlL']ratings = pd.read_csv(datadir+'BX-Book-Ratings.csv', sep=';', error_bad_lines=False, encoding="latin-1")ratings.columns = ['userID', 'ISBN', 'bookRating']Nous pouvons désormais inspecter le contenus de nos deux tables :
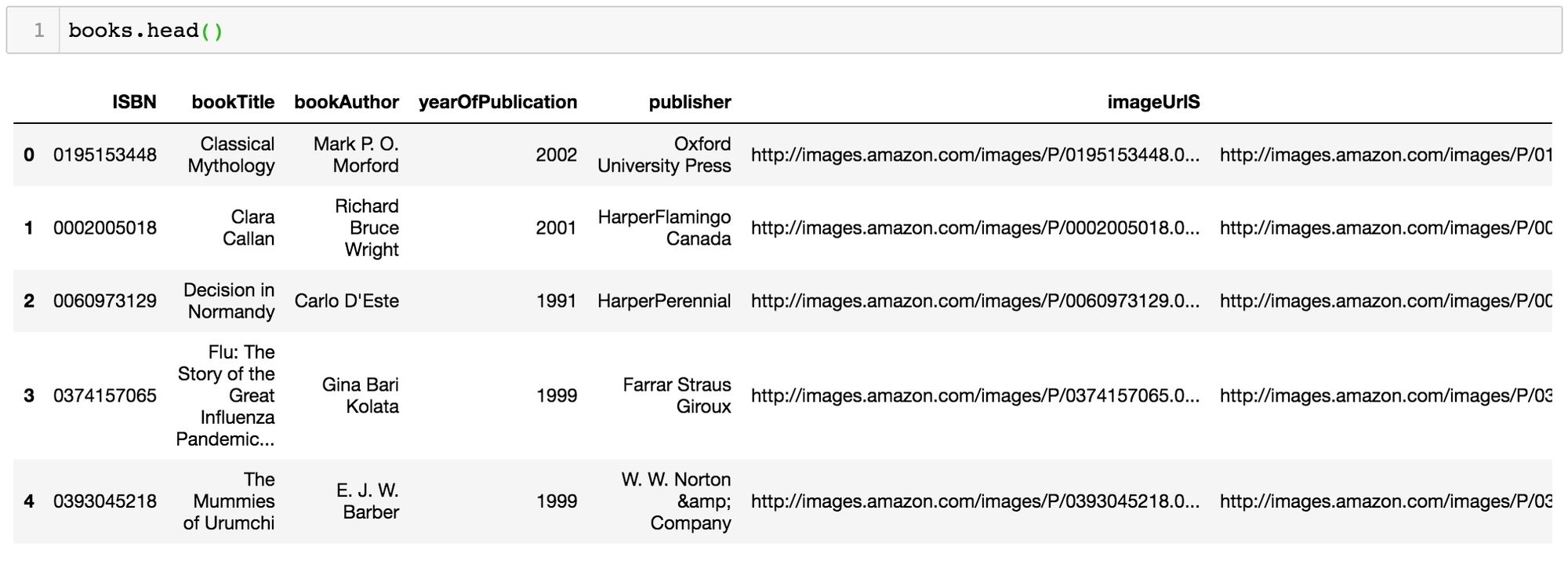
et
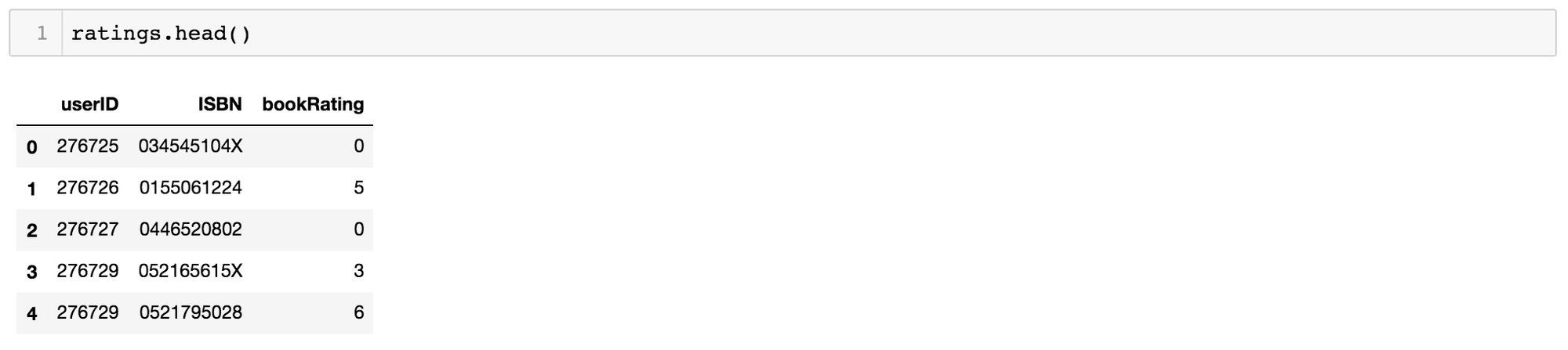
A moins que votre but ultime soir de pouvoir dire : "Voici la liste des livres que les utilisateurs ayant un historique de lecture similaire au vôtre peuvent ou non détester avec passion", vous souhaiterez probablement supprimer toutes les notes en dessous d’un certain seuil:
# Keep only Ratings above 5:ratings = ratings[ratings.bookRating > 5]De la même manière, je vais supprimer les colonnes dont nous n’aurons pas besoin dans la table "Books", m’assurer que chaque ISBN correspond à une seule entrée de livre et définir l’ISBN comme index du tableau:
columns = ['yearOfPublication', 'publisher', 'imageUrlS', 'imageUrlM', 'imageUrlL']books = books.drop(columns, axis=1)books = books.drop_duplicates(subset='ISBN', keep="first")books = books.set_index('ISBN', verify_integrity=True)Une étape supplémentaire de pré-traitement consiste à filtrer les livres qui ont été évalués par moins de trois utilisateurs. Ce filtre sera appliqué aux évaluations, plutôt qu’à la table Books:
# Keep only those books, that have at least 2 ratings:ratings_count = ratings.groupby(by='ISBN')['bookRating'].count().reset_index().rename(columns={'bookRating':'ratingCount'})ratings = pd.merge(ratings, ratings_count, on='ISBN')ratings = ratings[ratings.ratingCount > 2]ratings = ratings.drop(['ratingCount'], axis=1)print(ratings.shape[0])Cela nous laisse avec 207 073 notes de livres. Maintenant, formatons ces données de manière à pouvoir en calculer la similarité cosinus comme nous l’avons fait ci-dessus. Nous voulons pour cela que chaque ligne corresponde à un ISBN et que chaque colonne corresponde à un utilisateur qui a évalué au moins un livre parmi les ISBN que nous avons dans notre tableau.
import timestart = time.time()matrix = ratings.pivot(index='ISBN', columns='userID', values='bookRating').fillna(0)end = time.time()print('Time it took to pivot the ratings table: ', end - start)matrix.head()Bien évidemment, comme la plupart des utilisateurs n’ont pas lu la plupart des livres, le tableau contiendra principalement des zéros:
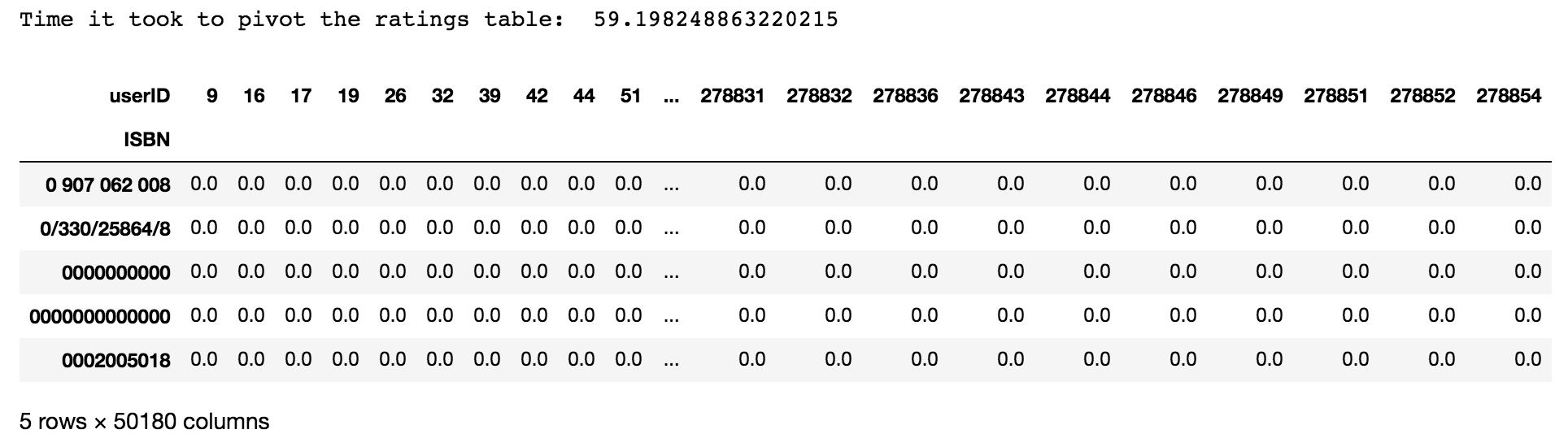
Les dimensions de la matrice finale sont 25159 x 50180, signifiant que nos recommandations seront basées sur 25159 books notés par 50180 lecteurs.
Maintenant, nous pouvons utiliser l’algorithme NearestNeighbors de sklearn pour trouver des recommandations de livres basées sur la similarité cosinus avec, comme exemple, le fameux “Harry Potter et la pierre du sorcier” susmentionnés (ou du moins en ce qui concerne le modèle, à la ligne indexée par son ISBN: 059035342X) . Étant donné que notre matrice est clairsemée, nous pouvons essayer de la convertir en un format spécial, le Compressed Sparse Row, pour voir si cela améliore les performances du modèle.
from scipy.sparse import csr_matrixfrom sklearn.neighbors import NearestNeighborsstart = time.time()book_matrix = csr_matrix(matrix.values)print('Time to convert to Compressed Sparse Row matrix format: ', time.time()-start)start = time.time()recommender = NearestNeighbors(metric='cosine', algorithm='brute', n_neighbors=10).fit(book_matrix)_, nearestBooks = recommender.kneighbors(matrix.loc['059035342X'].values.reshape(1, -1))print('Time to make a recommendation using the CSR matrix: ', time.time()-start)start = time.time()recommender = NearestNeighbors(metric='cosine', algorithm='brute', n_neighbors=10).fit(matrix)_, nearestBooks = recommender.kneighbors(matrix.loc['059035342X'].values.reshape(1, -1))print('Time to make a recommendation using the original matrix: ', time.time()-start)Time to convert to Compressed Sparse Row matrix format: 31.45536208152771Time to make a recommendation using the CSR matrix: 0.015137195587158203Time to make a recommendation using the original matrix: 6.317066431045532Le recours au Compressed Sparse Row nécessite de la préparation en amont, mais se traduit par un temps d’inférence beaucoup plus rapide lorsqu’il s’agit de générer réellement une recommandation. Faire tourner ce modèle de recommandation à partir de la matrice d’origine contenant tous les zéros nous aurait pris 6 secondes par recommandation, tandis que les 30 secondes nécessaires pour nettoyer les données ne le sont qu’à chaque fois que vous souhaitez mettre à jour les données sur lesquelles vous basez vos recommandations. Ce qui rend ce nettoyage rapidement rentable.
Voyons à présent si recommandations elles-mêmes sont pertinentes:
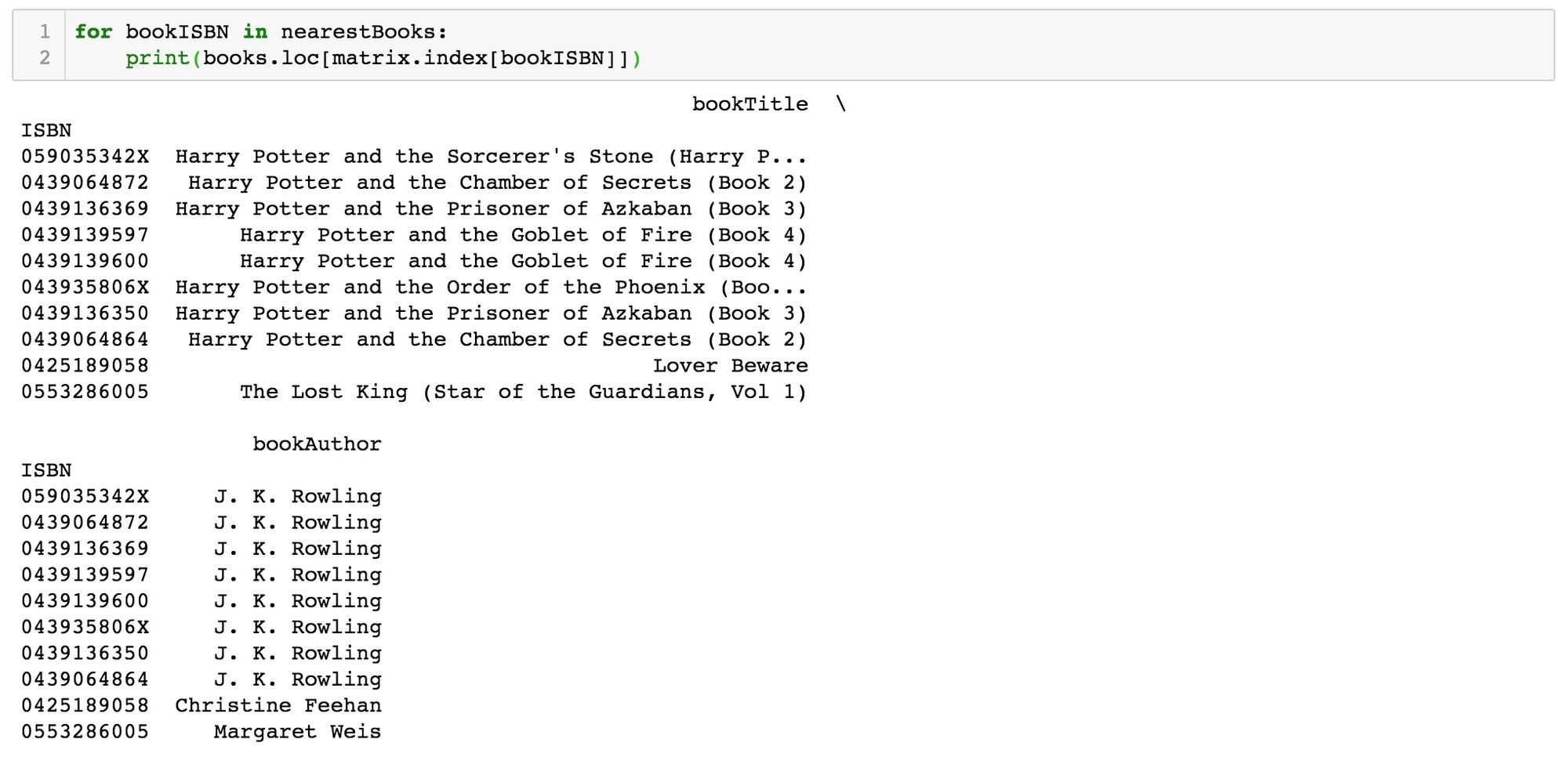
Le premier titre apparaissant dans la liste des livres les plus proches est, bien sûr, celui sur lequel nous voulons baser nos recommandations, Harry Potter et la pierre du sorcier (étant donné qu’il est également inclus dans notre matrice des notes). Les romans qui s’en rapprochent le plus sont, sans surprise, d’autres livres de Harry Potter, et, de manière plus surprenants, d’autres univers:

Okay.
Si vous pensiez que TensorFlow et PyTorch étaient utilisés exclusivement pour du deep learning, vous serez surpris: ces Frameworks peuvent être également utilisés pour calculer la similarité cosinus nécessaire à notre moteur de recommandation. Voyons comment cela peut être fait avec PyTorch sur une instance dédié Scaleway RENDER-S livrée avec un GPU NVIDIA P100:
import torch# In PyTorch, you need to explicitely specify when you want an # operation to be carried out on the GPU. device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")# Now we are going to simply append .to(device) to all of our torch # tensors and modules, e.g.:cos_sim = torch.nn.CosineSimilarity(dim=1, eps=1e-6).to(device)# We start by transferring our recommendation matrix to the GPU:start = time.time()torch_matrix = torch.from_numpy(matrix.values).float().to(device)print('Time to transfer the recommendation matrix to the GPU: ', time.time()-start)# Now, let's get our Harry Potter recommendationsstart = time.time()# The vector corresponding to "Harry Potter and the Sorcerer's Stone": ind = matrix.index.get_loc('059035342X')HPtensor = torch_matrix[ind,:].reshape(1, -1)# Now we can compute the cosine similarities:similarities = cos_sim(HPtensor, torch_matrix)_, nearestBooks = torch.topk(similarities, k=10)print('Time to make a recommendation with PyTorch: ', time.time()-start)Time to transfer the recommendation matrix to the GPU: 4.763129711151123Time to make a recommendation with PyTorch: 0.0011758804321289062Par rapport au meilleur résultat (la matrice nettoyée) sur le CPU, l’étape de préparation de la matrice prend 5,3 secondes au lieu de 31,5, et la recommandation elle-même ne prend que 0,003 seconde contre 0,015 sur le CPU.
Quand time = money, que représente pour votre business d’être 5 plus fois rapides ? 😉

Les conséquences de nos actions ou de notre inaction d’aujourd’hui ne feront que se multiplier au fil du temps. Alors demandons-nous: mon fournisseur cloud est-il vraiment durable ?
Dans cet article, nous allons distinguer les différentes méthodes d'autoscaling fournies par Kubernetes et comprendre les différences entre l'horizontal pod autoscaler et le vertical pod autoscaler.

Alors que chacun est appelé à raisonner ses consommations d’eau, une industrie méconnue avale des milliards et des milliards de litres en silence : les datacenters.